Arabok-e az arab számok?
Míg a világ nyelveinek írásán több tucat kisebb-nagyobb írásmód osztozik ma is, addig a számjegyek írását szinte teljes mértékben a magyarul arab számok néven ismert számjegyek uralják. Korábban azonban nagyon sok írásnak saját jelölése volt a számokra is. Hogyan, hol és mikor alakultak ki, illetve minek köszönhető az arab számjegyek átütő sikere?
Az „arab”számjegyek valójában nem az araboknál alakultak ki, hanem Indiában, és az írás elterjedéséhez képest viszonylag későn. A sumerek és az egyiptomiak is nagyjából az i.e. 3. évezred közepétől már használtak írást, és a számokat is jelölték. A következő 3000 évben népek tucatjai vették át tőlük, vagy alakították ki saját írásmódjukat és számjegyek jeleit, de a ma használt számjegyek története valójában csak i.sz. 500 körül kezdődött Indiában. Természetesen a babiloni, a görög, a római és a kínai matematikusok és csillagászok is használtak számokat, de az áttörő változást csak a számok helyi érték alapú lejegyzése hozta meg.

(Forrás: wikimedia commons / Euyasik)
A helyi érték alkalmazásának különlegessége, hogy radikálisan leegyszerűsíti a matematikai műveletek végrehajtását, ami e nélkül folyamatos bonyolult átalakításokat és átszámításokat kíván. A római számokkal is lehet például szorozni és összeadni, de ehhez a jelölt számokat „konkretizálni” kellett, például abakusz segítségével. (ilyesféle eszközöket már ősidők óta ismertek). A jól működő helyi érték alapú matematika feltétele pedig a nulla, de nemcsak a nulla (latin nullus, ’semmi’) fogalma, hanem annak jelölése is.
A zéró fogalmáról már a fent említett kultúrákban is tudtak, de rendszeres jelölése sosem terjedt el. A maják ugyan már i.e. 36-tól használtak jelölést a nullára, ez viszont akkor nem jutott, nem juthatott el az óvilágba. Indiában azonban már legalább valamikor az i.sz. 5. századtól elkezdték használni a nulla tízes számrendszer szerinti helyi értéki jelölését. Indiai matematikusok dolgozták ki a nulla alapvető algebrai és aritmetikai alkalmazását is (Brahmagupta, 628). Az indiai számokat és használatukat vette át a perzsa származású Abu Abdalláh Muhammad ibn Músza al-Hvárizmi (i.sz. 780 – 845).
Al-Hvárizmi Bagdadban élt és arab nyelven írta műveit. Bagdadban jelent meg A Számítás hindu számokkal című munkája is 825 körül, és ezzel az „arab” számok visszafordíthatatlanul elindultak hódítóútjukon. Nevéhez nemcsak ez, hanem az algebra és az algoritmus szavak származása is köthető, az előbbi egyik könyvcímének, az utóbbi pedig saját nevének rövidítéséből és latinosításából került be az európai nyelvekbe az első latin nyelvű fordítás után (1145). Maga a zéró szó szintén arab eredetű, a صفر ṣifr, ’üres’ szó olasz változata honosult meg különböző módokon az európai nyelvekben. (Az arab kifejezés egyébként pedig a szanszkrit sunya fordítása.)
A nagyon jó kulturális kapcsolatokkal rendelkező arab világ tudósai között gyorsan terjedt az új számjelölés, a távolsággal és az idővel azonban kicsit megváltoztak a számok formái. A hindu-arab számokként is ismert jelöléseknek három fontosabb változata létezik ma is: az indiai, a keleti arab és a nyugati arab. Európába e legutóbbi érkezett el, melyeket a 976-os kiadású Codex Vigilanus említ először.
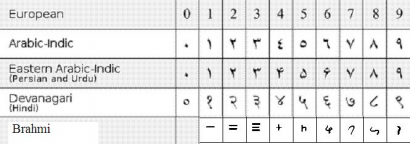
(Forrás: wikimedia commons, nyest)
Az új számjegyek európai meghonosodása lassú folyamat volt. A következő lökést a számjegyeket Észak-Afrikában elsajátító olasz matematikus, Leonardo Fibonacci 1202-ben kiadott Liber Abaci című könyve adta, de az általános elterjedés csak a nyomatatás feltalálása után – Gutenberg, c. 1440 – gyorsult fel. Angliában például 1445-ben, Magyarországon pedig V. László (1440-1457) rövid uralkodásának végén jelentek meg az arab számok először. Oroszország a 18. század végén, Nagy Péter uralkodása alatt, Kína és Japán pedig a 19. század végén kezdte el használni az arab számjegyeket. Ma már szinte minden ország és nyelv alapvetően a hindu-arab számokat használja, azoknak is túlnyomórészt az általunk is ismert nyugati arab változatát. Ez alól kivételt csak azok a nyelvterületek képeznek, ahonnan a nyugati arab számok korábbi változata történelmileg származik, tehát főleg az arab országok és India kulturális hatókörzete.
Ez utóbbi területhez főleg Dél-Ázsia és Délkelet-Ázsia tartozik, ahol sok nyelv a bráhmi családba tartozó saját írásmódot használ. Az indiai nyelveken kívül ilyen még például a burmai, a thai, a lao, és a khmer is. Ezek a nyelvek nem csak bráhmi írásra visszavezethető írásjelekkel rendelkeznek, de többségüknek saját, a hindu-arabhoz hasonló, helyi érték alapú számjegyeik is vannak. Ugyan ma már az európai számjegyek is általánosan ismertek ezeken a területeken is, de a hagyományos helyi számjegyek használta is él még. Például e nyelvek wikipédia szócikkei is gyakran a hagyományos számjegyeket használják, és a bankjegyek előlapján is gyakran találkozhatunk ilyen európaiak számára „felismerhetetlen" számokkal.

(Forrás: wikimedia commons)
A hindi nyelvű wikipédia is a dévanágari számokat használja, de az indiai bankjegyeken már csak a nyugati arab számok jelennek meg, pont azért, mert az indiai nyelvek többségének saját számjegyei vannak. A dévanágari számjegyekkel is találkozhatunk azért bankjegyeken, például a nepáli rúpiákon.
Az arab világban a számjegyek használata nem teljesen egységes. Egyiptomtól nyugatra az Európában is ismert nyugati arab számjegyek jellemzőek, a többi területen viszont a keleti arab számjegyek az általánosan elterjedtek. Ez a különbség az térség bankjegyeinek számjegyeiben is megmutatkozik. A keleti arab államok papírpénzének előlapján a keleti arab számjegyek szerepelnek, és csak a hátoldalukon láthatóak az európaiak számára is könnyen felismerhető nyugati arab számjegyek, míg Egyiptomtól nyugatra már a bankjegyeken is csak az utóbbi számokkal találkozhatunk.
A fent említett példák ellenére az arab számjegyek sikere szinte teljesnek mondható, és alapvetően a logikusságuknak, praktikusságuknak köszönhető.
Olvasói kérésre itt egy táblázat a számjegyek európai fejlődéséről:

Források:
http://mathforum.org/dr.math/faq/faq.roman.html#calc
http://www.omniglot.com/language/numerals.htm
http://www.skypoint.com/members/waltzmn/Mathematics.html
Kapcsolódó tartalmak:
Hasonló tartalmak:
Hozzászólások (121):
Követem a cikkhozzászólásokat (RSS)Az összes hozzászólás megjelenítése

@Akitlosz: És arra a világnapra megállna a Hold is az égen?
Mert ha nem, akkor bizony hiába mondod, hogy nem tartozik az a nap egyik hónaphoz se, a Hold bizony elkezd egy új holdhónapot.
A Hold Föld körüli keringési idejének (holdhónap) nem egész számú többszöröse a a Föld Nap körüli keringési ideje (év), sőt ezek egyike se egész számú többszöröse a Föld forgási ciklusidejének (nap), így hiába variálsz, az égbolthoz képest valahol szét fog mászni a naptár.
"A hold egy teljes ciklusának lineáris ideje 29.53059 napot tesz ki a mi megfigyelésünk szerint. Vagyis, a Hold 27.33 nap alatt kerüli meg a Földet, de a Föld is mozog a Nap körül, így összeadva a két mozgást az eredmény 29.53 nap. Ha átrágod magad a számításokon, akkor ez azt eredményezi, hogy körül-belül 12.368 megfigyelt lunáris ciklus esik egy 365.25 napos évre, de a Hold 13.36-szor kerüli meg a Földet évente."
hu.wiktionary.org/wiki/holdh%C3%B3nap
@Akitlosz: Egy tisztességes informatikus 1023-ig tud számolni az ujjain. :)
Csak el kell döntse, hogy melyik ujj melyik helyiérték, és a kinyújtott ujj azon a helyiértéken 1, a becsukott pedig 0.
Érthetőbben pl itt:
www.mathsisfun.com/numbers/binary-count-fingers.html
@Kormos:
Akkor jó.
Máris nyugodt vagyok.
No nem mintha, ha eddig nem az lettem volna.
@Akitlosz: Az ⅓ tökéletes pontossággal ábrázolható. Választhatsz kedvedre ⅓, 1/3, 1:3 stb. Még a számológép is ismeri, pl 1÷3 formában. A hányadosok értékét tökéleztes pontossággal megadhatjuk, tökéletes pontossággal ábrázolhatjuk, tökéletes pontossággal alkalmazhatjuk, még igazából tizedestört formában is. Akarsz egy nagy frászt? Még a 0,3̇ is tökéletesen pontos. Vagy ha jobban tetszik, 0,3̄-ként is írhatod. Mind pontos. Mind meghatározható. Mind alkalmazható. Sohasem hallottam még arról, hogy egy mérnöki probléma abból fakadt volna, hogy harmadolni kellett. Egyszerűen megteszik és kész. Tizes számrendszeren. Mivel pontosan ismerjük az értékét, nincs jelentősége annak, hogy van leírás, amiben végtelen tizedestört. Attól még ismerjük az értékét. A 60-as számrendszer sem adna semmi többet, mint a jelenleg is használt, nem végtelen leírási módok. Csak egy újabb leírási mód. Kiszámolni így is ki tudjuk, és dolgozni is tudunk vele. Semmi jelentősége annak, hogy helyiérték-alapú ábrázolásban hogy néz ki, vagy hogy nem.
@Kormos:
Nem.
De, 3,3-mal lehet pontosan számolni, a gépeknek is.
Az 1/3-dal meg nem. Legalábbis 2-es, 10-es számrendszerekben nem. Ha viszont az a 3,3 9-es számrendszerben van, akkor máris pontos számot jelöl, nem kerekített.
Na persze ez nem akkora súlyú probléma, hogy akárki is ettől ne tudna aludni. Nekem megteszi a 10-es számrendszer is, a rómaiaknak is megtette. Ez a cikk nem is erről szól, hanem a számjegyekről.
Nem tűnik akkora nagy világmegváltó durranásnak ez az arabnak titulált indinai jelölésmód.
Minek tíz jel a tízes számrendszerben való számoláshoz?
Az ókori egyiptomiak is tízes számrendszert használtak, aztán mégis elegendő volt nekik ehhez 7 fajta jel is.
A lényeg, amit akartam, akarok mondani, hogy két külön dolog a számolás és a számok jelölése.
@Kormos:
Csak kár, hogy a számoló- sőt a számítógépek sem ismerik a módszeredet.
Leírhatod, hogy ⅓ csak ezt nem fogják számként felismerni és értelmezni sem a számoló, sem a számítógépek és nem tudnak pontosan számolni vele 2,8,10,16 stb. számrendszerekben.
Arra csak a 3, 6,9,12, 60, 360 stb. számrendszerek alkalmasak.
Na persze fel lehet tenni a kérdést, hogy minek is akkora pontosság.
Hát ha lehet valamit pontosan is kiszámolni és pontatlanul is, akkor valószínű, hogy a pontos a jobb.
Na meg aztán valamiért a pontosan ki nem számolható π értékét is egyre pontosabban akarják kiszámolni. Azt minek, hova? Az összes iskolában is elég volt csupán annyi, hogy 3,14. Akinek nem ennyivel jött ki az eredménye ő biztosan valami hű de komoly számológépet használt, amelyik pontosabban tudta. A gyakorlatban sehova sem kell olyan pontossággal, amilyen pontossággal már ismert, aztán mégis sportot űznek belőle.
Na hát az ⅓ értéke viszont pontosan ismerhető, csak nem ábrázolható pontosan tízes számrendszerben.
Számít?
Hát ha egy csokit akarunk elosztani három gyerek között ...
akkor majd kiderül.
@Akitlosz: Miért? 3,3-at tudsz írni egy karakterben?
@Kormos:
"Hülyeség, bármilyen számrendszerben bármilyen osztás tökéletesen ábrázolható. Tizedestörtként nyilván nem ábrázolhatsz harmadok,"
Tehát nem hülyeség.
"de ez csak azért van, mert a harmad az nem tizedestört, hanem harmadostört. Ettől még ugyanúgy leírhatod tört alakban, és pontos lesz."
Akkor legyél szíves segítsél nekem!
Megmondanád, hogy az ⅓-ot merre találom a billentyűzeten?
A számológépé is jó. :-)
Tudsz egyáltalán írni ⅓-ot egy karakterben Controll+c, Controll+v módszer nélkül?
S akkor ez még csak az ⅓ volt, de mi van ha ⅔-ot akarnánk írni?
Na ennyire komoly és elterjedt a "harmadostörtek" használata. Még a tudományos számológépek sem ismerik. Tudományosan sem.
@Akitlosz: Magammal abszolút egyet értek. Ahogy mondtam, nem csak helyiérték alapú leírás van. Tény, hogy ha a harmadokat tizedekként próbálod leírni, végtelen szakaszos lesz, de semmi szükség másik számrendszerre ahhoz, hogy a harmadokat harmadokként írjuk le, mivel tizes számrendszerre is kész megoldásunk van arra, hogy a harmadokat harmadokként írjuk le, ez pedig pontosan az, hogy harmadokként írjuk le őket, pl.: ¹⁰/₃. Ez pedig pontosan olyan pontos, mint ha bármilyen más számrendszeren írnánk le harmadként.
@Kormos:
"Már bocsi, de ennek semmi értelme. Annyi van, hogy az egyik számrendszer helyiérték-alapú leírásában végtelen szakaszos lehet valami, ami a másiban nem az. "
Akkor most semmi vagy van?
Ha magaddal sem értesz egyet, akkor előbb magaddal vitatkozzál ne velem!
Igen, az az értelme, amire magad is rájöttél, ami után én leírtam, tehát ez máris nem semmi!
@Mackósajt:
"Az egyenlő hosszú hónap szintén nem lehetséges"
Simán lehetséges.
13X28=364.
A maradék egy nap pedig a "világnap" a Szilveszter, amelyik nem tartozik hónaphoz és héthez sem, csak az évhez.
Ez még több is mint lehetséges.
Annyira egyszerű, hogy az már nagyszerű.
@El Vaquero:
Szökőévre szükség van, de ez nem gond.
13 hónapos év esetén minden hónap egyenlően 28 napos, így minden hónap elseje vasárnapra esik.
Év végén meg van egy "világnapnak" nevezett ünnepnap, a Szilveszter.
Szökőévben pedig még egy világnap június 28-a és július 1-eje között.
És ennyi.
12 hónapos év esetén pedig a január, április, július, október kezdődik vasárnappal és ezek a hónapok 31 naposak, az összes többi 30 napos. Így minden évszak és minden negyedév is egyformán 91 napból áll, ugyanannyi munkanappal - a nemzeti ünnepeket nem számolva természetesen - a Szilveszter az év végén a szökőnap pedig június 30-a és július 1-eje között.
Ez a két legjobb naptárreform javaslat szerintem.
@Albu:
"még egy normális naptárreformnak (hogy a hét és az év napjai szinkronba kerüljenek) sincs esélye."
De nem kötelező, hogy minden ujj ugyanannyit jelentsen.
Ha a hüvelykujj 5-öt ér, akkor máris 18-ig tudunk számolni és mutogatni az ujjainkkal a két kezünkön.
@szigetva:
"még egy normális naptárreformnak (hogy a hét és az év napjai szinkronba kerüljenek) sincs esélye."
Ellenzik a vallási fanatikus országok. Vatikán, Amerikai Egyesült Államok. Pedig praktikus lenne és anyagi hasznot is hozna.
És a valóságot is jobban tükrözhetné, ha újra be mernék vezetni a 13-ik hónapot. Na ja az prímszám, de hát ha egyszer 13 hónap azaz Hold nap van a valóságban ...
Viszont cserében nem csupán az év, de minden hónap is szinkronba kerülne a hetekkel.
364=13X28=7X52.
Csak egyetlen nyamvadt nappal kell kezdeni valamit évente, de akkor meg úgyis mindenki ünnepel, mert éppen Szilveszter van, tehát amúgy sem sokan hívják azt a napot hétfőnek vagy éppen pénteknek, hanem Szilveszternek hívják.
@Akitlosz: Hülyeség, bármilyen számrendszerben bármilyen osztás tökéletesen ábrázolható. Tizedestörtként nyilván nem ábrázolhatsz harmadok, de ez csak azért van, mert a harmad az nem tizedestört, hanem harmadostört. Ettől még ugyanúgy leírhatod tört alakban, és pontos lesz.