Mi köze az Alzheimer-kórnak a Facebookhoz és a járványokhoz?
Lehetséges úgy átjutni egy városon, hogy közben egyetlenegy kocsmát se érintsünk? Körbe lehet-e járni Königsberg városát úgy, hogy minden hídon csak egyszer megyünk át? Mi köze az Alzheimer-kórnak a Facebookhoz? – A gráfelmélet mindezekre a kérdésekre megadja a választ.
A világon nagyjából bármi tekinthető a kommunikáció eszközének: a virágok színei, a madarak éneke, az idegsejtek közti szinapszisok az agyban és persze a szavak. Ahhoz pedig, hogy bármilyen egyedek képesek legyenek kommunikálni egymással, kapcsolat szükséges. Nem nagy meglepetés tehát, hogy az élettudományok mind inkább a kapcsolatok modellezésére alkalmas gráfelméletet helyezik a kutatások előterébe. Ennek segítségével leírhatók a kapcsolatok egy hálózat objektumai között – legyenek azok akár csatornák, internetes oldalak, hangyák vagy neuronok. És ezáltal modellezhető a kommunikáció is ezek között az objektumok között.
Ismert tény, hogy az Alzheimer-kórban szenvedők agyában fehérjék rakódnak le, ami gátolja az idegsejtek kommunikációját. A legújabb kutatások pedig azt mutatják, hogy a gráfelmélet révén új rálátást kaphatunk arra, hogy milyen meghibásodott kapcsolatok okozzák a progresszív memóriavesztést az Alzheimer-kórban szenvedőknél. De mi is az a gráfelmélet?
Königsberg hídjai és a gráfelmélet
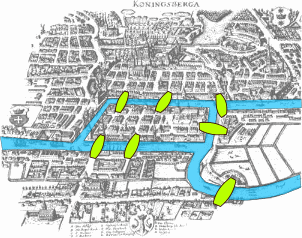
A gráfelmélet eredetét keresve a 18. századi Poroszországba, Königsberg városába kell visszatérnünk. Itt oldotta meg Leonard Euler a königsbergi hidak matematikai problémáját. És ez a felfedezés nagy hatással volt az úgynevezett hálózatelmélet fejlődésére.
Königsberget a Prégel folyó ágai négy részre osztják, ezeket a területeket pedig hét híd köti össze egymással.
A probléma – amit Euler előtt senki nem tudott megoldani – pedig az volt, hogy visszaérkezhetünk-e a kiindulópontunkhoz úgy, hogy mindegyik hídon csak egyszer megyünk át.
Euler, ahelyett, hogy ész nélkül kezdett volna fel-alá járkálni a városban, hogy kipróbálja a lehetőségeket, inkább papírral és ceruzával látott neki a problémának. És ezzel a geometria egy új területének alapjait rakta le, amelynek segítségével nemcsak Königsberg hídjainak a problémája, de minden más, hasonló jellegű probléma is megoldható.
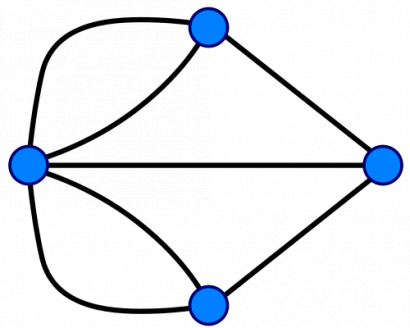
Euler észrevette, hogy a dolgok összekapcsolása kiemelkedő jelentőséggel bír a probléma megoldásában: a város különböző területeit csomópontokként (csúcsokként), az őket összekötő hidakat pedig élekként ábrázolta. Ahhoz, hogy olyan körutazást tegyünk, amelynek során nem fordulunk vissza, minden csúcsba (és csúcsból) páros számú él vezet. Königsbergben azonban a csúcsokból páratlan számú út indul ki. Így lehetetlen körbejárni a várost úgy, hogy minden hídon csak egyszer megyünk át.
Euler 1786-os halála óta az általa megalapított geometriai irányzat hatalmas fejlődésnek indult, amit mi sem bizonyít jobban, mint hogy az internetnek is az euleri matematika az alapja.
Hálózatok mindenütt
A hálózatelmélet egyik új irányzatát Watts és Strogatz 1998-as cikke hozta el, amelyben három különböző típusú hálózatról – a földigiliszta agyáról, az USA elektromos hálózatáról, illetve egy internetes moziadatbázisban szereplő színészek együttműködési kapcsolatairól – bizonyították be, hogy ugyanolyan felépítésűek: kisvilág-tulajdonságúak. Ez azt jelenti, hogy az egyes csúcsok viszonylag kevés lépésben elérhetőek.
Ismerős lehet ez a gondolat például a híres „hat lépés távolság” (six degrees of separation) elnevezésű feltevésből E szerint a világon bárki bárkivel kapcsolatba hozható egy ismeretségi láncon keresztül, amelyben a két végpont között maximum öt csúcs (azaz közbülső ember) van. Magyarán bárki ismerősének az ismerősének az ismerősének az ismerősének az ismerőse az amerikai elnök.
Később az is kiderült, hogy a természetben található közel összes hálózat kisvilág-tulajdonságú; talán éppen azért, mert ez biztosítja a legjobb információátadási hatékonyságot egy relatíve „olcsó” (kevés nódusból álló) hálózaton. Az is kiderült, hogy az emberi agy is kisvilág-tulajdonságú.
Az Alzheimer-kórban, illetve a skizofréniában szenvedő betegek agyában ez a kisvilág-felépítésű hálózat elkezd véletlenszerűen működni. A gráfelméleti modell szerint az agyban találhatók olyan csomópontok, amelyek a különböző agyi területek kommunikációját biztosítják; a halántéklebenyben található például a memória központja. A gráfelmélet segített annak a felfedezésében, hogy a fali lebenyben azonosítsanak egy másik központot („átkapcsoló állomást”), ami biztosítja a halánték- és a homloklebeny kommunikációját.
Tehát az Alzheimer-kórt kutatók is a kisvilág-felépítés modelljét használták, hogy feltárják az egészséges és a kóros elváltozást mutató agy szerkezeti különbségeit. Az Alzheimer-kórosok agya elkezd véletlenszerűen működni, így az egyes agyterületek normális kommunikációja sérül, illetve esetlegessé, hatékonytalanná válik.
De nem csak az idegtudományokban használható a gráfelmélet! A különböző internetes közösségi oldalak, amilyen például a Facebook vagy a Twitter, szintén kisvilág-tulajdonságúak. Így például valakinek a facebookos szociális hálózata alapján az epidemiológusok meg tudják állapítani, hogy mennyi esélye van elkapni egy fertőző betegséget. A Facebook tehát a járványok terjedésének megjósolásában, illetve megakadályozásában is segíthet.
Forrás
What links Alzheimer's disease, the bridges of Königsberg and Twitter?