Fekete, fehér, igen, nem? A χ²-próba
Ismét Bergengóciába látogatunk! Van-e ebben a távoli, de gazdag országban összefüggés a piréz nyelvtanulás és a nyelvek iránti érdeklődés között? A férfiak szavaznak inkább a baloldalra, vagy a nők? A statisztika pillanatok alatt választ ad a hasonló kérdésekre!
Módszertannal és kísérlettervezéssel foglalkozó sorozatunkban ezúttal egy olvasói kérést teljesítünk. Mi fán terem a χ²-próba [khi-négyzet-próba], hogyan kell értelmezni azt, ha ez a fogalom előkerül valamilyen szakszövegben? Senki se aggódjon – habár cikkünkből kiderül, hogyan kell a χ²-próbát elvégezni, ehhez egy fia képletre sem lesz szükség. A modern számítástechnika segítségével már ez is lehetséges...

(Forrás: Wikimedia Commons / Ken Thomas)
Mire jó?
Eddig még nem tárgyaltunk egyetlen konkrét statisztikai eljárást sem, de azért is érdemes épp a χ²-próbával kezdeni, mert könnyen megérthető: nem kell hozzá semmi különös, csak egy táblázat, benne számokkal. Ha már használtunk valamilyen táblázatkezelő programot legalább egyszer, akkor tulajdonképpen mindent tudunk, ami ennek a fura nevű próbának a megértéséhez kell.
Akkor lehet a χ²-próbát végrehajtani, ha olyan kérdéseink vannak, amelyek esetében csak néhány válaszlehetőség létezik, és a válaszokat nem lehet számegyenesen vagy legalább hozzávetőlegesen nagyság szerinti sorba rendezni. Megfelelőek például az igen-nem kérdések, a politikai pártállás, az etnikai hovatartozás, vagy éppen a nem. Ha ellenben olyan adataink vannak, amelyeket nagyság szerinti sorba lehet rakni, akkor más próbákat érdemes használni, amelyeket most nem fogunk részletezni. Nagyság szerint sorbarendezhető például az életkor, az elvégzett iskolai osztályok száma, a politikusok rokonszenvessége ötfokú skálán, vagy akár a szókincs.

(Forrás: Wikimedia Commons / liuhsiaofen / CC BY-SA 2.0)
A χ²-próbának három fajtája van: a függetlenségvizsgálat, a homogenitásvizsgálat és az illeszkedésvizsgálat. A két előbbit teljesen egyforma módon kell elvégezni, és leggyakrabban ezt az eljárást szokás χ²-próba alatt érteni. Mi is ezt fogjuk elsőként részletezni, de lejjebb az illeszkedésvizsgálatról is szót ejtünk.
Ha van néhány különböző csoportunk – például férfiak és nők, vagy fehér, fekete és ázsiai emberek, vagy Nyest-olvasók és nem Nyest-olvasók –, és van egy tulajdonságunk, ami a fentebbi feltételnek megfelel, akkor a homogenitásvizsgálat megmondja, hogy a csoportjaink eltérnek-e egymástól e tulajdonság tekintetében. Mit lehet például így vizsgálni? Bergengócia két nagy pártja a Bergengóc Népi-Nemzeti Összefogás és a Bergengóc Forradalmi Munkapárt. (A történelem kacskaringói miatt az előbbi a baloldali, az utóbbi a jobboldali párt – Bergengócia már csak ilyen.) A férfiak és a nők ugyanolyan mértékben szavaznak a két pártra, vagy van valamilyen nemi különbség a két csoport között? Erre a kérdésre választ adhat a homogenitásvizsgálat.
A függetlenségvizsgálat viszont két tulajdonság egymással való összefüggéséről mond valamit egy csoporton belül. Ha van két olyan kérdésünk, ahol mindkettőre igen/nem választ lehet adni, és a két kérdés között szeretnénk összefüggést keresni, akkor ez a próba tökéletes. De lássunk erre egy részletesebb példát, konkrét számadatokkal!
Elő a táblával
Tegyük fel, hogy megkérdezzük kedves bergengóc válaszadóinkat, hogy beszélnek-e pirézül, és érdeklik-e őket a nyelvek. Most az egyszerűség kedvéért mindkét kérdésre csak igen-nem válaszokat fogadunk el tőlük. Vajon van-e kapcsolat a nyelvek iránti érdeklődés és a piréz nyelvtudás között? Ez egy egyszerű függetlenségvizsgálat.
A válaszok gyakoriságait ügyesen táblázatba foglalhatjuk, ennek a neve kontingenciatábla. Attól függően, hogy hány rubrikába írhatjuk be a számokat, m*n-es kontingenciatáblának nevezik a táblázatot. Ez például egy 2*2-es tábla (számadataink teljességgel kitaláltak):
| Érdeklik a nyelvek | Nem érdeklik a nyelvek | |
| Beszél pirézül | 31 | 18 |
| Nem beszél pirézül | 78 | 93 |
Tehát 31 fő mondta azt, hogy beszél pirézül és érdeklik a nyelvek, 18 fő mondta, hogy beszél pirézül, de nem érdeklik a nyelvek, és így tovább. Ha ránézünk a táblázatra, láthatjuk, hogy a várakozásainknak viszonylag megfelelőek a számok: akik beszélnek pirézül, azokat inkább érdeklik a nyelvek, akik nem beszélnek pirézül, azokat kevésbé érdeklik a nyelvek. (És összességében kevesebben vannak azok, akik pirézül beszélnek...) De ez az eltérés tényleg szignifikáns – mint azt a korábbi részekben már említettük – vagy pusztán a véletlen ingadozás eredménye? Megmondja a χ²-próba!
Kattintgassunk lelkesen
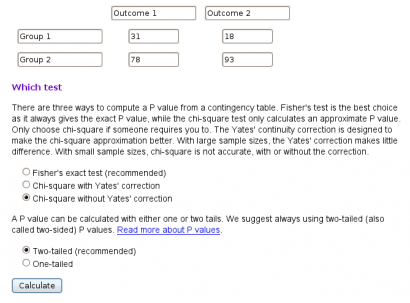
A próbát akármelyik modern táblázatkezelővel végrehajthatjuk, de valószínűleg még egyszerűbb, ha fogunk egy webes χ²-számoló alkalmazást, és beleírogatjuk a rubrikákba a számokat. Rengeteg ilyet találhatunk az interneten, főleg angol nyelven. Vegyük mondjuk ezt a weboldalt! Másoljuk bele a fentebbi táblázatunk számadatait, majd válasszuk ki a Chi-square without Yates’ correction és a Two-tailed opciókat, végül kattintsunk a Calculate gombra! (Első nekifutásra elég annyit tudni, hogy ezek az opciók elvégzik nekünk a χ²-próbát, de lejjebb több ki fog derülni.)
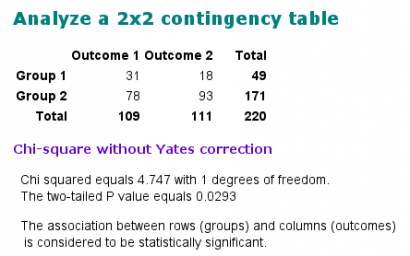
Kapunk egy csomó adatot, de a legtöbbet figyelmen kívül hagyhatjuk. A próba tulajdonképpeni eredménye a p-érték (angolul p value vagy P value). Ez egy 0 és 1 közé eső szám, és minél kisebb, annál jobb. A p-érték azt mutatja, hány százalék a valószínűsége annak, hogy az eredményünk pusztán a véletlen ingadozásnak tudható be, és nincsen semmilyen összefüggés a két tényezőnk között. Lássuk, pontosan mire jutottunk!
A p-érték 0,0293. Ezt százzal megszorozva megkapjuk a százalékértékünket: 2,93% az esélye annak, hogy az eredmény a véletlennek tudható be. Ez jó vagy rossz? A gyakorlatban a kutatók az 5%-os (avagy 0,05-ös) küszöböt szokták használni: ha 5%-nál kisebb a p-érték, akkor beszélnek szignifikáns különbségről. Tehát itt sikerült szignifikáns különbséget találnunk! Kimondhatjuk, hogy fiktív mérésünk szerint van összefüggés a piréz nyelvtanulás és a nyelvek iránti érdeklődés között. Ugyanezt végigjátszhatjuk a Forradalmi Munkapártos kérdésfeltevéssel is.
Van mááásik!
A gyakorlatban a fenti típusú χ²-próba fordul elő gyakrabban, de létezik egy másik típus is, ezt χ²-illeszkedési vizsgálatnak (chi-square goodness of fit test) hívják. Ha előre tudjuk, hogy milyen gyakoriságokat várhatunk egy méréstől, akkor ezen próba segítségével meg lehet mondani, hogy a ténylegesen mért adatok illeszkednek-e az elvárt adatokhoz.
Vegyünk például egy szép formás bergengóc binárt és dobjuk fel százszor! (A binár Bergengócia hivatalos pénzneme.) Azt gondoljuk, hogy egyenlő arányban fogunk fejet és írást kapni: 50 fejet és 50 írást. De ha mondjuk 42 fejet és 58 írást kaptunk, az azt jelenti, hogy a pénzérménk aszimmetrikus, vagy csak épp véletlenül így alakult a mérésünk, és nem tükröz valós különbséget? Elvégre egy kis véletlen ingadozás normális.
Ha az online χ²-alkalmazásban az observed (angolul ’mért’) és az expected (angolul ’elvárt’) szavakkal találkozunk, akkor az ezt a típusú próbát számolja ki. Próbáljuk ki! Ezen az oldalon az alsó táblázatba írogathatjuk a számokat.
Itt is a p-érték a fontos. Mennyit kaptunk? Ha minden igaz, 0,1096 körüli értéket. Az 10,96%, ami nagyobb, mint a bevett 5%-os küszöb. Tehát ebben az esetben azt mondanánk, valószínűleg csak véletlenül fordult elő a pénzfeldobás során a vártnál több írás. Nem kell másik pénzérmét keresnünk...
Szabad-e?
Vigyázat, sok statisztikai program minden próbát lelkesen kiszámol, és nem hívja fel külön a figyelmet arra, ha a feltételek nem teljesülnek!
A statisztikai módszereknek gyakran van egy vagy több végrehajtási feltételük. Ha a feltétel nem teljesül, akkor a próbát ugyan elvégezhetjük, de az eredmény félrevezető lehet. A χ²-próbának nagyon egyszerű végrehajtási feltétele van. Egyszerűen csak meg kell néznünk a kontingenciatáblát, és ha valamelyik rubrikában ötnél kisebb számot látunk, akkor inkább hanyagoljuk a χ²-próbát!
De mit lehet tenni ilyenkor? Sajnos rengeteg népszerű eljárásnak nagyon szigorúak a végrehajtási feltételei, úgyhogy a statisztikusok mindent bevetnek, hogy olyan újabb eljárásokat alkossanak, amelyek hasonlóan működnek, csak enyhébb feltételekkel lehet elvégezni őket. Azokat a próbákat, amelyek kevéssé érzékenyek ilyen tekintetben, robusztus eljárásoknak hívják. Talán a legnépszerűbb robusztus χ²-helyettesítő a Fisher-féle egzakt-próba vagy röviden Fisher-egzakt-próba. Ezt a próbát sajnos sem a Microsoft Excel, sem az OpenOffice vagy LibreOffice Calc nem tudja alapkiszerelésben, de mindegyikhez telepíthetőek ingyenes kiegészítők, amelyek képesek a számítás elvégzésére. Ezeket a cikk végén szereplő linkgyűjteményben megtalálhatjuk. Ha nem szeretnénk ilyesmivel szöszögni, számos weboldal kiszámolja nekünk az eredményt.
Sajnos a webes alkalmazások nagy kontingenciatáblákat általában nem tudnak kezelni, ami nem is csoda, hiszen a Fisher-egzakt-próba ilyen esetben rendkívül számításigényes. A régebbi statisztikakönyvek épp ezért általában 2*2-es táblaméret fölött mindig a χ²-próbát ajánlják. Ma már az asztali számítógép kiszámol bármit, legfeljebb malmozik rajta egy ideig...
Az irodalomban gyakran lehet találkozni még a χ²-próba Yates-korrekciójával. Ezt a Fisher-egzakt-próbához hasonlóan akkor lehet használni, ha a sima χ²-próba végrehajtási feltételei nem teljesülnek. Ma már nem igazán ajánlják ezt a fajta korrekciót, mert túl szigorú.
Ha a példánkban mért számadatainkon kiszámoljuk a Fisher-egzakt-próbát, körülbelül 0,035-öt kapunk. Ez egy szignifikáns érték, csakúgy, mint a sima χ²-próba esetében.
Tényleg elég ennyi?
Már tudjuk, hogyan kell végrehajtani ezeket az eljárásokat, és hogyan kell értelmezni az eredményt. De hiányérzetünk támadhat... A számítógép esetünkben mindvégig a fekete doboz szerepét játszotta, amiben rejtély, mi történik belül. Beleraktuk az adatainkat, azt mondtuk neki, hogy számolja ki a χ²-próbát, és aztán értelmeztük a kiadott eredményt. De ettől mi magunk továbbra sem fogjuk tudni kiszámolni a próbát. Baj-e ez?
Gyakran maguk a kutatók sem ismerik az általuk végrehajtott bonyolultabb statisztikai eljárások minden számítási részletét (hacsak történetesen nem statisztikusok), hiszen mindennek megvan a bevett végrehajtási menete, amit kézzel úgy is rendkívül macerás lenne reprodukálni. Az egyetemi képzés során gyakran csak az egyszerűbb módszereket veszik végre lépésről lépésre, a többinél csak a végrehajtási feltételeket és az eredmény értelmezését tanítják. A χ²-próba végrehajtásához elég a négy alapművelet rafinált használata, így ha valaki szeretné maga is kiszámolni, a lentebbi linkek között talál anyagot hozzá. A többieknek bőven elég a fentieket tudni...
Hasznos információk, letöltések (javarészt angolul)
Online χ²-próba és Fisher-egzakt-próba 2*2-es kontingenciatáblán
Online Fisher-egzakt-próba 2*n-es kontingenciatáblán. Ne írjunk bele nagyon nagy számokat!
Fisher-egzakt-próba kiegészítő Excelhez és Calchoz (az utóbbi kicsit bonyolultabb)
χ²-illeszkedésvizsgálat végigszámolva, korpusznyelvészeti példával
Mindkét fajta χ²-próba végigszámolva, magyarul!
Miért ne használjuk a χ²-próba Yates-korrekcióját (haladóknak)




@Nyenyi: Ha el tudja magyarázni ezt a bonyolult módszert egyszerűbben, írását szívesen közzétesszük.
Az elején sokkal egyszerűbben le kellett volna írni, hogy miről szól az egész.
Hosszú cikk, mégsincs benne, hogy mit számol a khí négyzet próba...
A p-érték pedig nem azt adja meg, hogy milyen valószínűséggel van véletlen zaj miatt az eredményünk, hanem hogy a véletlen milyen valószínűséggel produkálna legalább olyan extrém eredményt, mint amit ténylegesen kaptunk.