Egyszerű ötletekből tudományos felfedezés?
Hogyan születnek a tudományos felfedezések? A tudomány félistenei vagy halandó emberek jönnek rá a misztikusnak látszó összefüggésekre?
Sokszor azt gondoljuk, hogy a tudományos felfedezések valamilyen isteni szikra, valamilyen különleges ajándék révén történnek meg. Az igazán nagy tudósok, amilyen Newton vagy Einstein számunkra, földi halandók számára elérhetetlen magasságokban vannak, már-már mitikus hősök, akiknek a képességeik és a tetteik is emberfelettiek. Kérdés, hogy jó-e ha így képzeljük el a tudományt.
Adam Savage válasza egy egyértelmű nem. A televíziós műsorvezető, a MythBusters (kb. ’mítoszírtók’, magyarul Állítólag) című műsor egyik állandó szereplője a YouTube-on is megtalálható műsorában megpróbálja lehozni a földre a tudományos felfedezéseket. Az alábbi videóban három olyan példát mesél el a tudomány történetéből, amelyek segítenek megérteni számunkra, hogy hogyan is működik a tudományos felfedezés.
Az egyik legviccesebb dolog az emberi agy működésével kapcsolatban – mondja Savage –, hogy nem tudjuk kontrollálni az a folyamatot, ahogyan az agyunk tárolja és összekapcsolja egymással a különböző tényeket, tapasztalatokat, történeteket. Bizonyos dolgok akár évekig is megragadhatnak a fejünkben, mielőtt rájönnénk, valójában miért is érdekelnek minket, miért is olyan fontosak a számunkra, hogy megjegyezzük őket.
A három történet közül az első ezt a folyamatot mintázza. A történet főhőse Richard Feynman (1918–1988) a 20. század egyik legnagyobb hatású elméleti fizikusa. Kisgyerekként egyszer apjával sétálni indultak egy húzós kocsi és egy labda társaságában. Séta közben a kis Feynman azt figyelte meg, hogy amikor meghúzza a kocsit, a rajta levő labda hátragurul egészen a húzós kocsi végébe. Ekkor megkérdezte az apját: „Apa, miért megy a labda hátra a kocsiban?” Mire az apja azt felelte. „Hát fiam, ezt hívják tehetetlenségnek.” Mivel a választ nem értette teljesen, visszakérdezett: „De mi az a tehetetlenség?” Mire az apja azt válaszolta: „Tehetetlenségnek nevezték el a tudósok azt a jelenséget, amikor elindítod előre a húzós kocsidat, és a rajta levő labda elindul hátrafelé. De valójában senki sem tudja, hogy mi az.”
Ezek után Feynman felnőtt, diplomákat szerzett az M.I.T.-n és a Princetonon, megfejtette a Challenger űrsikló tragédiájának a titkát és végül megkapta a fizikai Nobel-díjat a szubatomi részecskék mozgásának leírásáért. Mégis azt a bizonyos apjával folytatott beszélgetést tekintette később élete fordulópontjának. Története azt illusztrálja, hogy a legegyszerűbb kérdések azok, amelyek eljuttathatnak minket az emberi tudás végső határáig. És ő oda akart elérni, és el is ért.
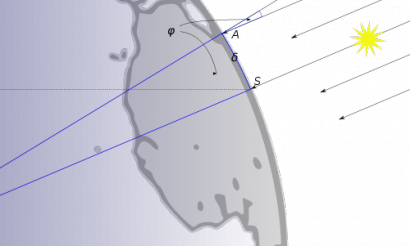
A következő példa, amit Savage említ, Eratoszthenész (i.e. 276–i.e. 194) ókori görög matematikus, földrajztudós, csillagász története. Ő volt a híres alexandriai könyvtár egyik könyvtárosa. Rengeteg tudományos felfedezést tett, de az, amelyik miatt az utókor még ma is emlékszik rá, egy levéllel kezdődött. Könyvtárosként kapott egy levelet az Alexandriától délre fekvő Szüéné (ma Asszuán) városából. Ebben a levélben volt egy tény, ami szöget ütött Eratoszthenész fejében. A levélíró azt említette, hogy napforduló idején, amikor délben belenézett a kútjába, látta az árnyékát a kút fenekén, és azt is észrevette, hogy a feje eltakarja a Napot.
Nem árt tudni, hogy a felfedezés, amelyet – tévesen – Kolumbusz Kristófnak tulajdonítanak, már ekkor ismert volt: a Föld gömbölyű. Arisztotelész óta ezt minden tanult ember tudta, így maga Eratoszthenész is. Arisztotelész be is bizonyította ezt egy igen egyszerű megfigyeléssel: a Föld a Holdon kör alakú árnyékot vet. És az egyetlen forma, aminek minden esetben kör alakú az árnyéka, az nem más, mint a gömb. Quod erat demonstrandum: a Föld gömbölyű. Azt azonban senki nem tudta ekkor még, hogy mekkora is.
Egészen addig, amíg Eratoszthenész meg nem kapta azt a bizonyos levelet. Ebből az derült ki, hogy a Nap pontosan Szüéné városa felett járt, amikor a levél írója a kútba nézett. Erasztothenész még egy másik tényt is tudott: azt, hogy ha Alexandriában ugyanakkor leszúrunk a földbe egy pálcát pontban délben, akkor az árnyékot fog vetni, amiből tudta, hogy a napsugarak beesési szöge ilyenkor 7,2°. Azt is tudta, hogy a Föld gömbölyű. Már csak arra volt szüksége, hogy megtudja, hogy a két város milyen távol fekszik egymástól. Tehát arra volt szüksége, hogy lemérje Szüéné városának és Alexandriának a távolságát. És ez persze meg se kottyant neki, hiszen földrajztudós is volt (ő használta először a geográfia kifejezést). Alexandria és Szüéné között húzódott egy kereskedelmi útvonal, amelynek a hosszát pontosan lehetett tudni: ez 500 mérföld volt. Ezek után felállított egy aránypárt: a két város távolsága úgy aránylik a Föld kerületéhez, mint a 7,2°-os beesési szög a 360°-hoz, a teljes körhöz. A 360-nak 50-ed része a 7,2, tehát a Szüéné–Alexandria távolságot megszrozva 50-nel, megkapjuk a Föld kerületének nagyságát: 25000 mérföld. Ez az eredmény 1%-os hibahatáron belül van a valódi kerület méretéhez képest. És ezt a felfedezést Eratoszthenész 2200 évvel ezelőtt tette.
Manapság olyan világban élünk, ahol több milliárd dolláros eszközökkel kutatunk a Higgs-részecskék után. Olyan részecskéket fedezünk fel, amelyek átlépik a fénysebességet. És mindezek a felfedezések azért lehetségesek, mert az elmúlt pár évtizedben a technika hatalmas fejlődésen ment keresztül. De az emberiség történetének nagyobb részében mégiscsak olyan felfedezéseket tettünk, amelyekhez elég volt a szemünket és a fülünket – no meg az eszünket használni.
Ezt példázza Armand Fizeau (1819–1896) története is, aki kísérleti fizikusként dolgozott Párizsban. Az elsődleges feladata az volt, hogy mások korábbi kísérleti eredményeit pontosítsa, bizonyítsa. Ez egy kicsit úgy hangzik, mintha „futottak még”-kategóriás alak lett volna, de valójában az ilyenfajta munka a tudomány lényegéhez tartozik. Ugyanis a nem tekinthető tudományos ténynek az, ami nem erősíthető meg a kísérletek megismétlésével.
Fizeau Galileinek a fénysebességgel kapcsolatos kísérleteivel foglalkozott. Galilei kidolgozott egy fantasztikus kísérletet: két ember áll egymással szemben, és mindketten egy-egy lámpát tartanak a kezükben, és hol az egyikük, hol a másikuk villantja fel a lámpát. Ezek után megismételték a kísérletet két, egymástól két mérföldnyi távolságban levő dombtetőn. Galilei feltevése az volt, hogy amennyiben a fénynek van mérhető sebessége, akkor a dombtetőn némi késést kellene tapasztalnia a másik ember lámpájából jövő fény esetében. De a fény még Galilei észjárásánál is gyorsabb volt. Azt tételezte, hogy a fény sebessége legalább tízszerese a hang sebességének.
Fizeau tisztában volt mindezzel. Párizsban élt, ami egy elég nagy város volt már akkor is. Ő a két világító állomáshelyét 5,38 mérföld távolságra helyezte egymástól. És megoldotta Galilei problémáját egy viszonylag egyszerű segédeszközzel. Fogott egy fogaskereket, és ezt arra használta, hogy kis adag fénycsóvákat küldjön a mérőállomásra. Egy lámpát helyezett a fogaskerék mögé, így amikor azt elkezdte forgatni, a fény a fogaknál nem tudott továbbhaladni, a réseknél viszont igen. Ezeket a fényjeleket küldte az 5 mérföldnyire levő tükör felé, ami visszatükrözte ezeket a fénynyalábokat, amelyek a fogaskerék foghíjain visszajutottak az ő szemébe.
Az érdekességet akkor tapasztalata, amikor egyre gyorsabban kezdte el pörgetni a fogaskereket. Olyan volt, mintha egy ajtó elkezdett volna becsukódni. Miért történt ez? Mert a fénycsóva már nem azon a lyukon ért vissza hozzá, amin elment, és visszafelé beleütközött egy fogba. És ha elég gyorsan pörgette a fogaskereket, akkor úgy tűnt, az elnyeli a visszatükrözött fénycsóvákat.
Ezek után a két állomáshely távolságának, a fogaskerék sebességének, illetve fogainak számának ismeretében kiszámolta a fény sebességét – a valóságoshoz képest 2%-os eltéréssel. És ezt 1849-ben csinálta.
És ez a nagyszerű a tudományban: amikor nem értünk egy elképzelést, visszamehetünk az időben, és megnézhetjük, hogy hogyan fedezték azt fel, hogyan alakult ki. Mindig érdemes megismerni a felfedezések történetét: hogyan jöttek rá arra a bizonyos dologra, ami általuk vált ismertté. És miért jó, ha megismerjük, hogyan gondolkodtak maguk a felfedezők? Mert ezáltal rájöhetünk, hogy nem is voltak olyan csodabogarak, hogy ők is úgy gondolkodtak, ahogyan mi, ők is csak emberek voltak.
Nagyon félrevezető, amikor az egyes tudományágakat az emberek egymástól független fekete dobozoknak tekintik. Valójában a tudományterület sokkal jobb kifejezés, mert talán jobban érzékelteti, hogy a tudomány összefüggő, egymással határos területek megismeréséről szól. És ez a terület nyitott, ahol mindnyájan felfedezők vagyunk. Az igazi felfedezők azok, akik kíváncsibbak, mint az átlagos ember, ők ezért jobban észreveszik a jelenségeket.
Forrás




Az említett kétkezes 65 éves korában halt meg, egy baleset következtében kifejlődő "jóindulatú" agydaganat műtétjében.
Valóban a szüntelen kíváncsiság a tehetség legfontosabb komponense. S ez is az állatavilágból ered. Az az egyed tudott legbiztosabban túlélni, amelyik először is minél több dolgot észrevett, ami hatással lehet ett rá. Utána nem nyugodott addig, amíg rá nem jött, hogy a káros hatásokat (az ő fajtájának testi adottságaival) hogyan lehet legjobban kivédeni, a hasznosakat meg a saját javára fordítani. Az embernek (legalábbis a "nyugati" civilizációban) már ritkán vannak mindennapos (éhezés-fázás) túlélési gondjai, így a kíváncsiság részben már elszakadt a saját test fenntartásának a problémájától.
Mindez azonban csak a jobbkezes átlagemberre igaz. A balkezes néha, esetleg, de a nagyon ritka valódi kétkezes talán? mindig olyan képességeknek is a birtokában van, amelyekről a jobbkezes csak álmodhat. Ezeknél a két agyfél differenciálódása elmosódik és úgy tűnik, hogy sokkal jobban működnek együtt. Egyetlen ilyen embert ismertem. Elképesztő memóriája és fejszámolási képessége volt. A fejszámolásra rákérdeztem, hogyan csinálja? Fogalmam sincs, felelte, ezen még sose gondolkoztam. De ha papír-ceruzával számolok, akkor már én is úgy csinálom, és ugyanolyan lassan, ahogy az iskolában tanultam.
Az érdekes az volt, hogy a szorzás-osztás, hatványozás (második hatványig) és gyökvonás (négyzetgyökig) CSAK a négyjegyűekig terjedt ki. Ötjegyűt bármivel már akkor sem szorzott be fejben, ha 10.002-vel kellett volna szorozni.
Hiába vagyok szuper kíváncsi (jobbkezes), ennek a titkát megfejteni nem tudtam soha.
Ez az ember a második, a budapesti származású izraeli férjem volt. A kétkezességét és a képességeit azonban eddig senki (a tőlem származó 3 utódja sem) örökölték. Eddig 11 leszármazottja van - mind "jó átlag" és mind jobbkezes.
@hegyaljai: Ha megnézed a filmet a TEDen (www.ted.com/talks/how_simple_ideas_lead_to_scientific_discoveries.ht), láthatod, hogy 2011 novemberében vették fel. Akkor egy ideig úgy tűnt, tényleg ilyet mértek Svájc és Olaszország közt. Azóta kiderült, hogy mégsem. De ezt nem kérheted számon egy a múltban elhangzott előadáson.
Tiltakoznék a szöveg következő része ellen:
"Olyan részecskéket fedezünk fel, amelyek átlépik a fénysebességet. "
Akkor most ez múlt idő?
Akkor, ha jelen idő, akkor hol zajlik ez?
Akkor most ez egy bizonyosság, akkor igazolás nélkül nem sokat ér.