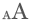Három évtized után végre újra találtak egy különleges ötszöget
Megtalálták a 15. olyan ötszöget, amellyel hiánytalanul le lehet fedni egy síkot anélkül, hogy azok átfednék egymást vagy köztük rés maradna – harminc éve nem találtak hasonlót. Minden három- és négyszög képes hiánytalanul kitölteni a síkot, de ennél több szöggel rendelkező síkidomok már nem: például egy egyenlő oldalú ötszög sem (de egy egyenlő oldalú hatszög igen).
A sík síkidomokkal való lefedésének (illetve terek testekkel való kitöltésének) problémáját a matematikában tesszalációnak nevezik. A szó a latin tessella szóból ered, mely agyagból, kőből vagy üvegből készült mozaikkockát jelent. A szakterület tudományos eredményeit a gyakorlatban ma is a mozaikkészítés, térkövezés vagy csempézés során lehet felhasználni, de fontos szerepe van bizonyos természeti jelenségek (kristályképződés, növények felépítése, habképződés stb.)
Ami az ötszögetket illeti, először 1918-ban fedeztek fel öt különböző ötszögtípust, amivel a sík kitölthető. Ezután kerek öt évtizedig úgy hitték, hogy több nincs is, míg 1968-ban találtak újabb hármat, majd 1975-ben még egyet., majd ugyanebben az évben egy amatőr matematikus még négyet, 1985-ben pedig találtak még egyet.
További részleteket is megtudhatunk a The Guardian cikkéből.